Drawing A Slope Field
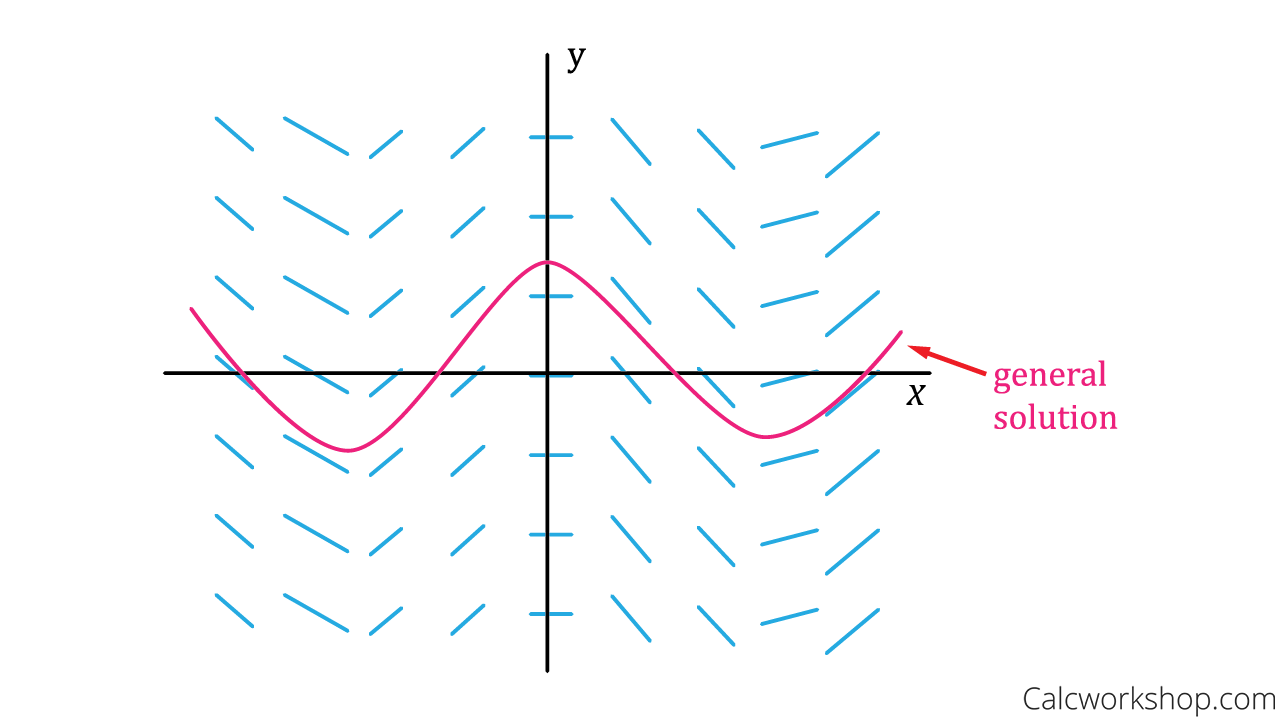
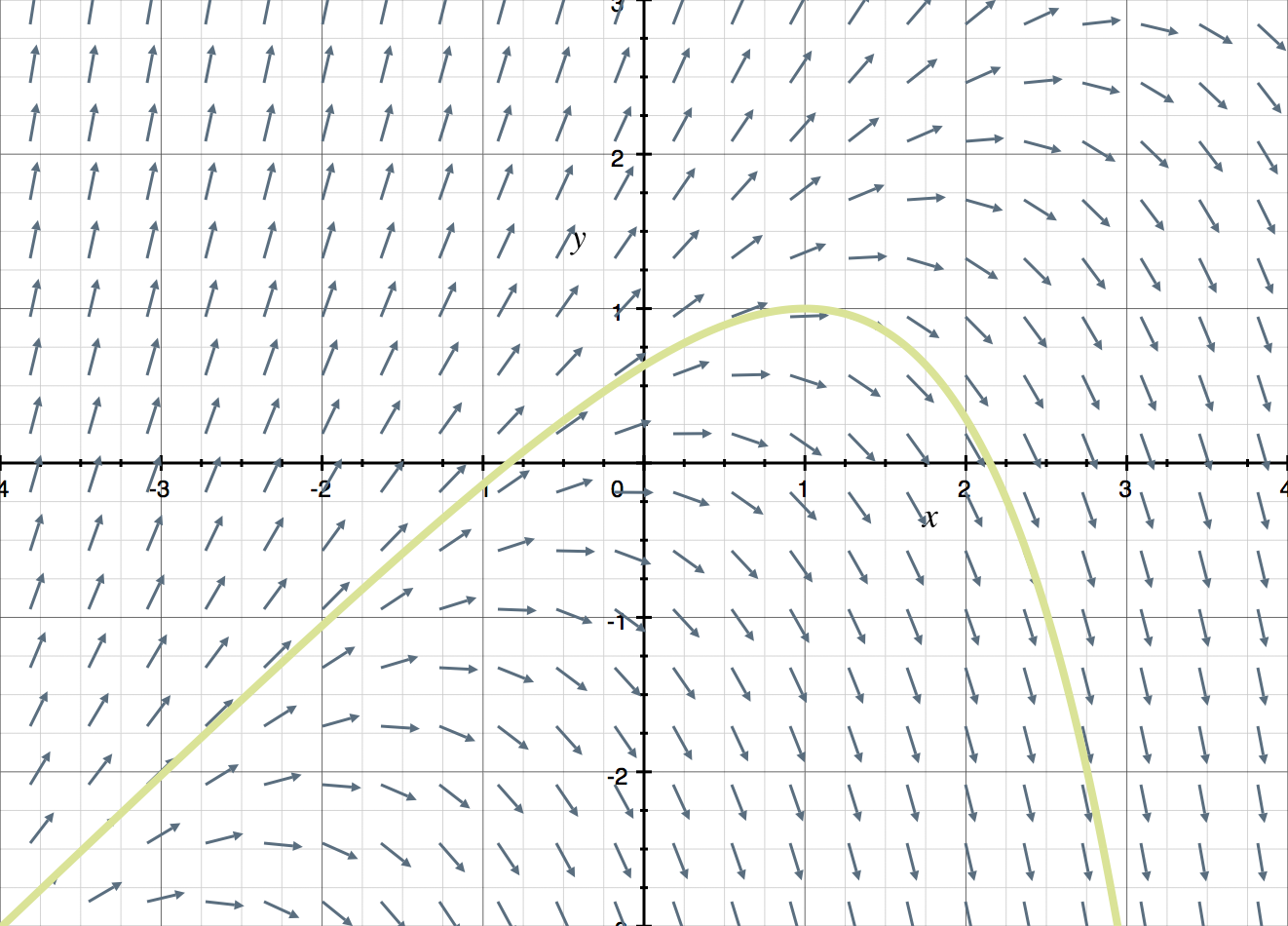
Drawing A Slope Field - Web draws the slope (direction) field for the given differential equation y' = f(x,y).the movable black point sets the initial condition of an approximated particular solution drawn with euler's method. A direction field (or slope field / vector field) is a picture of the general solution to a first order differential equation with the form. Using a visualization of a slope field, it is easy to. Web how to sketch the slope field brian mclogan 1.27m subscribers join subscribe like share save 3.7k views 4 years ago differential equations learn how to create slope fields and sketch the. Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. D y d x = x + y a Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Sketching slope fields slope fields introduction worked example: Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. The pattern produced by the slope field aids in visualizing the. A direction field (or slope field / vector field) is a picture of the general solution to a first order differential equation with the form. The vectors in a slope field are usually drawn without arrowheads, indicating that they can be followed in either direction. Web draws the slope. That's the slope field of the equation. In other words, \(f(x,y)\) is the slope of a solution whose graph runs through the point \((x,y)\). And this is the slope a solution \(y(x)\) would have at \(x\) if its value was \(y\). Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at. Web brian mclogan 1.29m subscribers 3.7k views 5 years ago differential equations learn how to create slope fields and sketch the particular solution to a differential equation. The slope field is utilized when you want to see the tendencies of solutions to a de, given that the solutions pass through a certain localized area or set of points. Wolframalpha.com type. The vectors in a slope field are usually drawn without arrowheads, indicating that they can be followed in either direction. Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. So each individual point of a slope field (or vector field) tells us the slope. Take the example of dy dx at (3,4). Web 5 years ago observe that you can draw infinitely many possible graphs for a given slope field. We'll illustrate this with a simple example: Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y). The pattern produced by the. The vectors in a slope field are usually drawn without arrowheads, indicating that they can be followed in either direction. Using a visualization of a slope field, it is easy to. Web 5 years ago observe that you can draw infinitely many possible graphs for a given slope field. The slope field is utilized when you want to see the. Take the example of dy/dx at (3, 4). See how we match an equation to its slope field by considering the various slopes in the diagram. Web brian mclogan 1.29m subscribers 3.7k views 5 years ago differential equations learn how to create slope fields and sketch the particular solution to a differential equation. In other words, \(f(x,y)\) is the slope. Web you are essentially correct. Web a slope field is a visual representation of a differential equation in two dimensions. Edit the gradient function in the input box at the top. We'll illustrate this with a simple example: Discover any solutions of the form y= constant. Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. Web brian mclogan 1.29m subscribers 3.7k views 5 years ago differential equations learn how to create slope fields and sketch the particular solution to a differential equation. We'll learn in a few sections how to. That's the slope field of the equation. Take the example of dy/dx at (3, 4). The beauty of slope field diagrams is that. We'll learn in a few sections how to solve this kind of equation, but for now we can't get an explicit solution. Web this calculus video tutorial provides a basic introduction into slope fields. Slope field from equation worked example: Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. At a point \((x,y)\), we plot a short line with the slope \(f. Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y). Match a slope field to a differential equation. Learn how to draw them and use them to find particular solutions. Take the example of dy dx at (3,4). Web a slope field is a visual representation of a differential equation in two dimensions. For instance, suppose you had the differential equation: Web 5 years ago observe that you can draw infinitely many possible graphs for a given slope field. That's the slope field of the equation. In other words, \(f(x,y)\) is the slope of a solution whose graph runs through the point \((x,y)\). This shows us the rate of change at every point and we can also determine the curve that is formed at every single point. Web given an ordinary differential equation y^'=f(x,y), the slope field for that differential equation is the vector field that takes a point (x,y) to a unit vector with slope f(x,y). Edit the gradient function in the input box at the top. Sketching slope fields slope fields introduction worked example:
Sketch the slope field and sketch the particular equation YouTube

Calculus AB/BC 7.3 Sketching Slope Fields YouTube
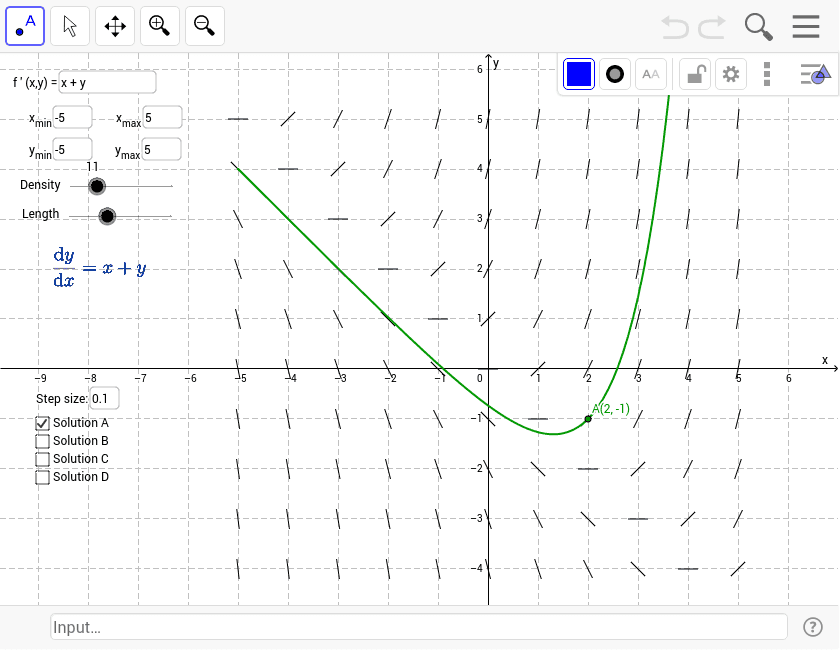
Slope field plotter GeoGebra
Slope Fields Calculus YouTube
Slope Fields
How to sketch direction fields — Krista King Math Online math help

Worked example slope field from equation AP Calculus AB Khan

Slope Fields_Example 2 on how to sketch a slope field YouTube
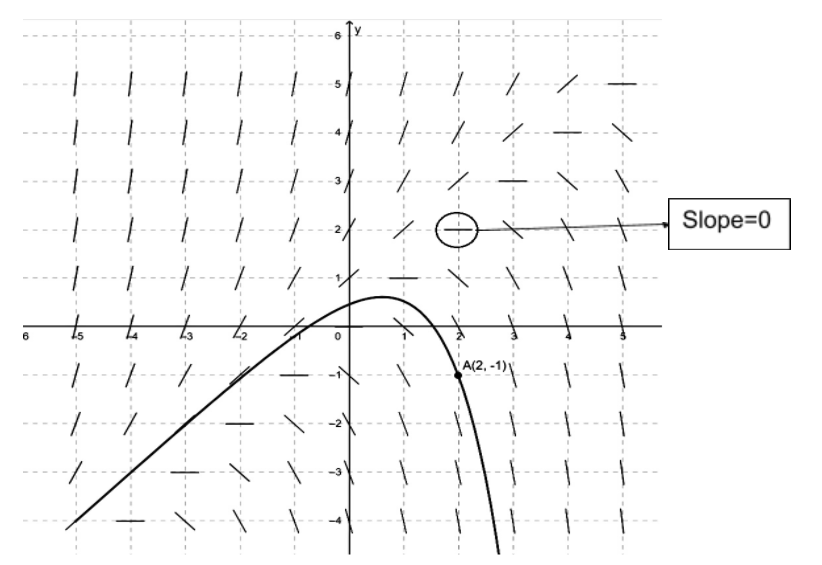
How do you draw the slope field of the differential equation \\[{{y

PPT Slope Field & Particular Solutions PowerPoint Presentation ID
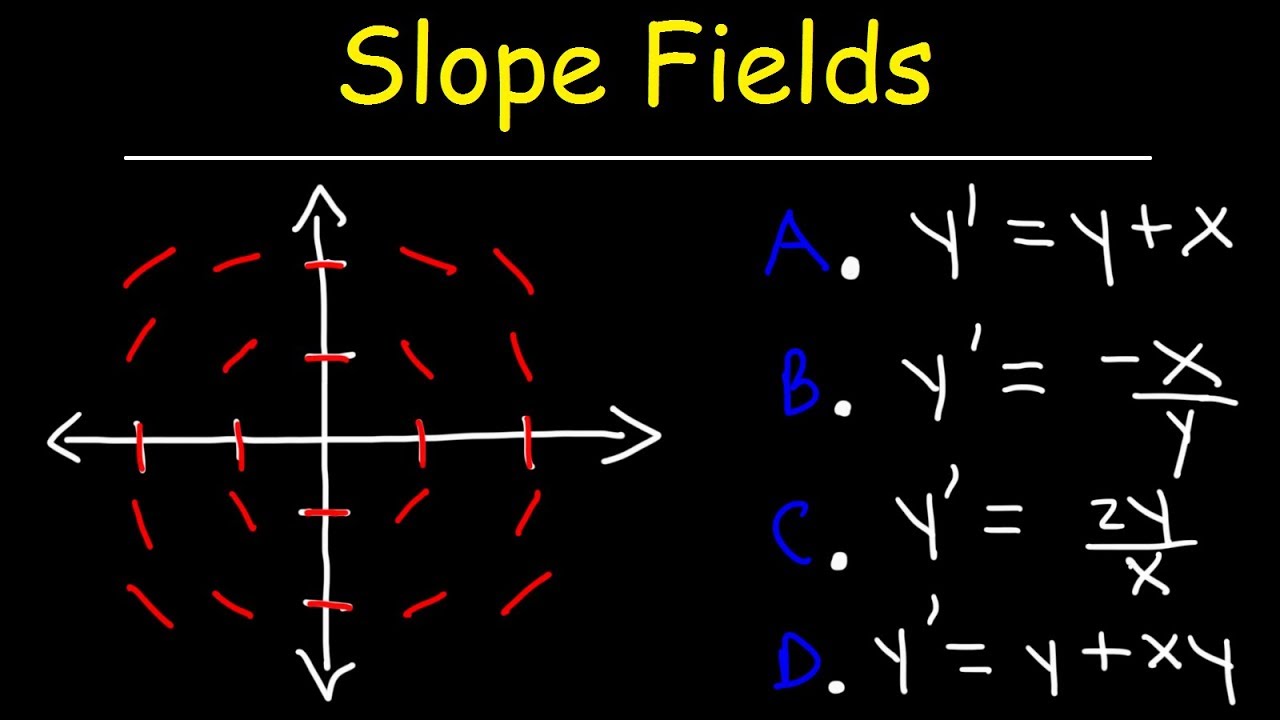
Forming A Slope Field Slope Fields & Equations Slope Fields & Equations Google Classroom Which Differential Equation Generates The Slope Field?
So Each Individual Point Of A Slope Field (Or Vector Field) Tells Us The Slope Of A Function.
For Dy Dx X2 −2, This Would Be Slope Field X2 −2.
Web Draws The Slope (Direction) Field For The Given Differential Equation Y' = F(X,Y).The Movable Black Point Sets The Initial Condition Of An Approximated Particular Solution Drawn With Euler's Method.
Related Post: