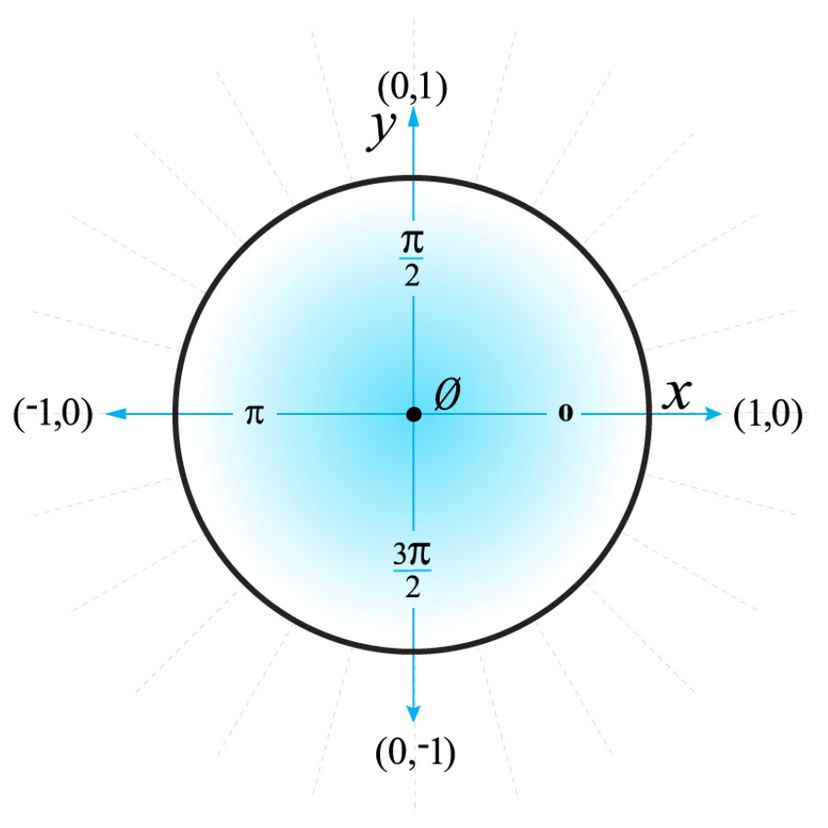
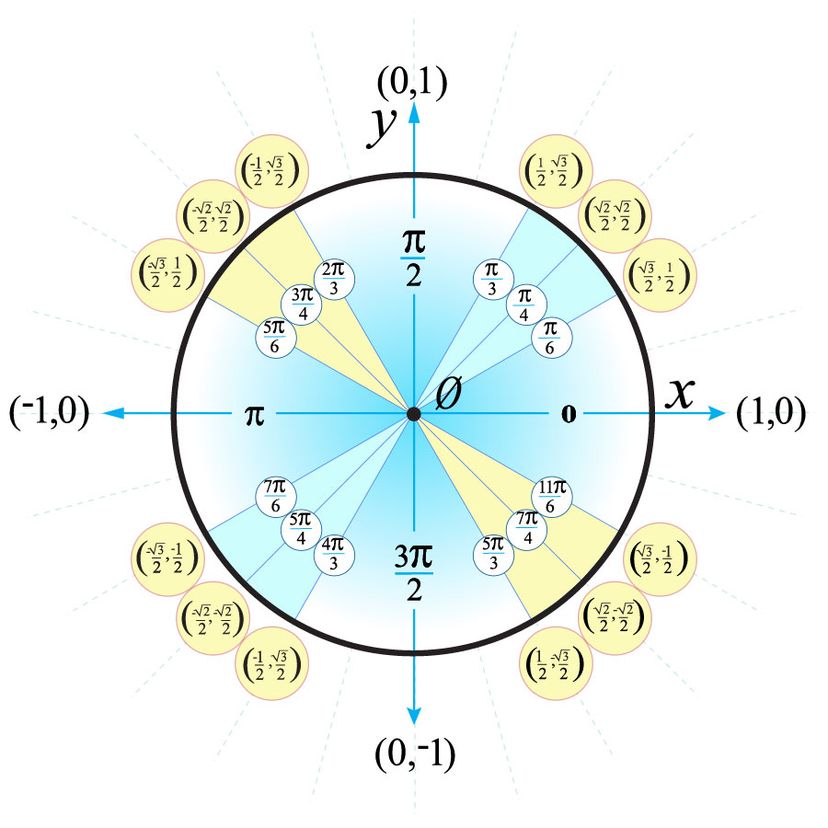
Unit Circle Drawing
Unit Circle Drawing - A unit circle is a circle of unit radius, i.e., of radius 1. Web unit circle and radians. So why is it so useful? Because that's the radius of the circle! Let (x, y) be the endpoint on the unit circle of an arc of arc length s. If \((x,y)\) are the coordinates of a point on the circle, then you can see from the right triangle in the drawing and the pythagorean theorem that \(x^2 +. X^2+y^2=1 x2 + y2 = 1. Θ=−320d exercises sketch each of the following angles in standard position. The equation of the unit circle is \(x^2+y^2 = 1\). Animation of the act of unrolling the circumference of a unit circle, a circle with radius of 1. Web a unit circle is a circle that is centered at the origin and has radius 1, as shown below. Just draw a brief sketch.) 1. Θ=−320d exercises sketch each of the following angles in standard position. If \((x,y)\) are the coordinates of a point on the circle, then you can see from the right triangle in the drawing and. Web updated september 17, 2021 trigonometry interactive the unit circle makes things easier, not harder. Let (x, y) be the endpoint on the unit circle of an arc of arc length s. X^2+y^2=1 x2 + y2 = 1. A negative angle is measured in the opposite, or clockwise, direction. We “wrap” the number line about the unit circle by drawing. In a circle or on a graph. Here's how i remember how to draw a unit circle. The unit circle plays a significant role in a number of different areas of mathematics. X 2 + y 2 = 1 2 but 1 2 is just 1, so: This line is at right angles to the hypotenuse at the unit circle. X 2 + y 2 = 1 2 but 1 2 is just 1, so: A unit circle is a circle of unit radius, i.e., of radius 1. A negative angle is measured in the opposite, or clockwise, direction. Web the unit circle is a circle of radius 1, centered at the origin of the (x,y) ( x, y) plane.. The unit circle is generally represented in the cartesian coordinate plane. Web to define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure 2. Web illustration of a unit circle. Web explore math with our beautiful, free online graphing calculator. Web the cool thing about a. Web a unit circle is a circle with a radius measuring 1 unit. How to memorize the unit circle In mathematics, a unit circle is a circle of unit radius —that is, a radius of 1. X2 + y2 = 1 equation of the unit circle also, since x=cos and y=sin, we get: Using the formula s = r t,. Just draw a brief sketch.) 1. How to memorize the unit circle Using the formula s = rt, and knowing that r = 1, we see that for a unit circle, s = t. A unit circle is a circle of unit radius, i.e., of radius 1. Web the cool thing about a unit circle (a circle with radius one),. (do not use a protractor; Web explore math with our beautiful, free online graphing calculator. For a given angle θ each ratio stays the same no matter how big or small the triangle is trigonometry index unit circle Web using the unit circle diagram, draw a line “tangent” to the unit circle where the hypotenuse contacts the unit circle. (cos. We “wrap” the number line about the unit circle by drawing a number line that is tangent to the unit circle at the point \((1, 0)\). Web a unit circle is a circle that is centered at the origin and has radius 1, as shown below. The unit circle is simple, it's a circle with a radius of 1. (do. Web unit circle trigonometry drawing angles in standard position examples the following angles are drawn in standard position: It describes all the negatives and positive angles in the circle. (cos (θ))2 + (sin (θ))2 = 1 a useful identity Web illustration of a unit circle. We can see things in their simplest form. \sin^2 (\alpha) + \cos^2 (\alpha) = 1 sin2(α) + cos2(α) = 1. Web unit circle trigonometry drawing angles in standard position examples the following angles are drawn in standard position: The unit circle is generally represented in the cartesian coordinate plane. Let (x, y) be the endpoint on the unit circle of an arc of arc length s. Web interactive unit circle sine, cosine and tangent. Θ=−320d exercises sketch each of the following angles in standard position. Web to define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in figure 2. Web pythagoras pythagoras' theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides: It is important because we will use this as a tool to model periodic phenomena. We “wrap” the number line about the unit circle by drawing a number line that is tangent to the unit circle at the point \((1, 0)\). If \((x,y)\) are the coordinates of a point on the circle, then you can see from the right triangle in the drawing and the pythagorean theorem that \(x^2 +. (cos (θ))2 + (sin (θ))2 = 1 a useful identity Animation of the act of unrolling the circumference of a unit circle, a circle with radius of 1. Let's get an intuition of the unit circle by using the interactive below. This line is at right angles to the hypotenuse at the unit circle and touches the unit circle only at that point (the tangent point). Sine, cosine and tangent sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle:How to Use the Unit Circle in Trigonometry HowStuffWorks

Unit circle Solved Examples Geometry Cuemath
Unit Circle Quadrants Labeled / The Unit Circle CK12 Foundation As
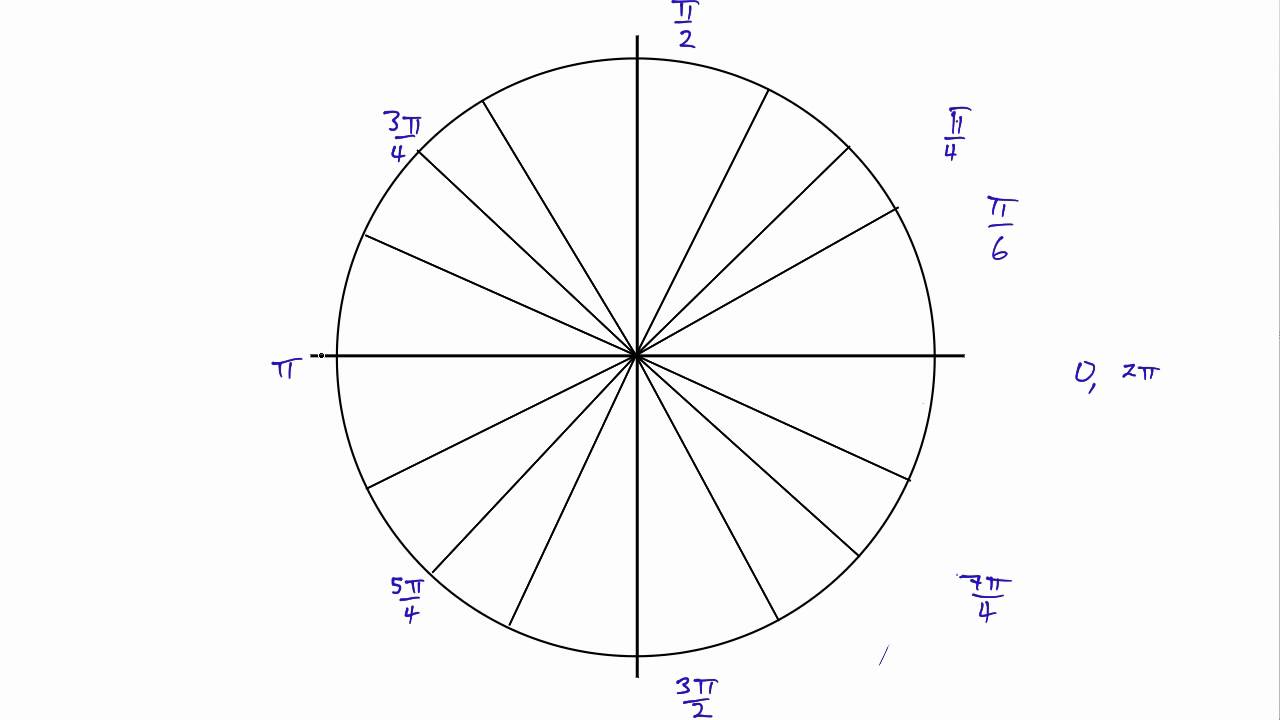
Drawing a Unit Circle YouTube

Unit Circle Quick Lesson Downloadable PDF Chart · Matter of Math
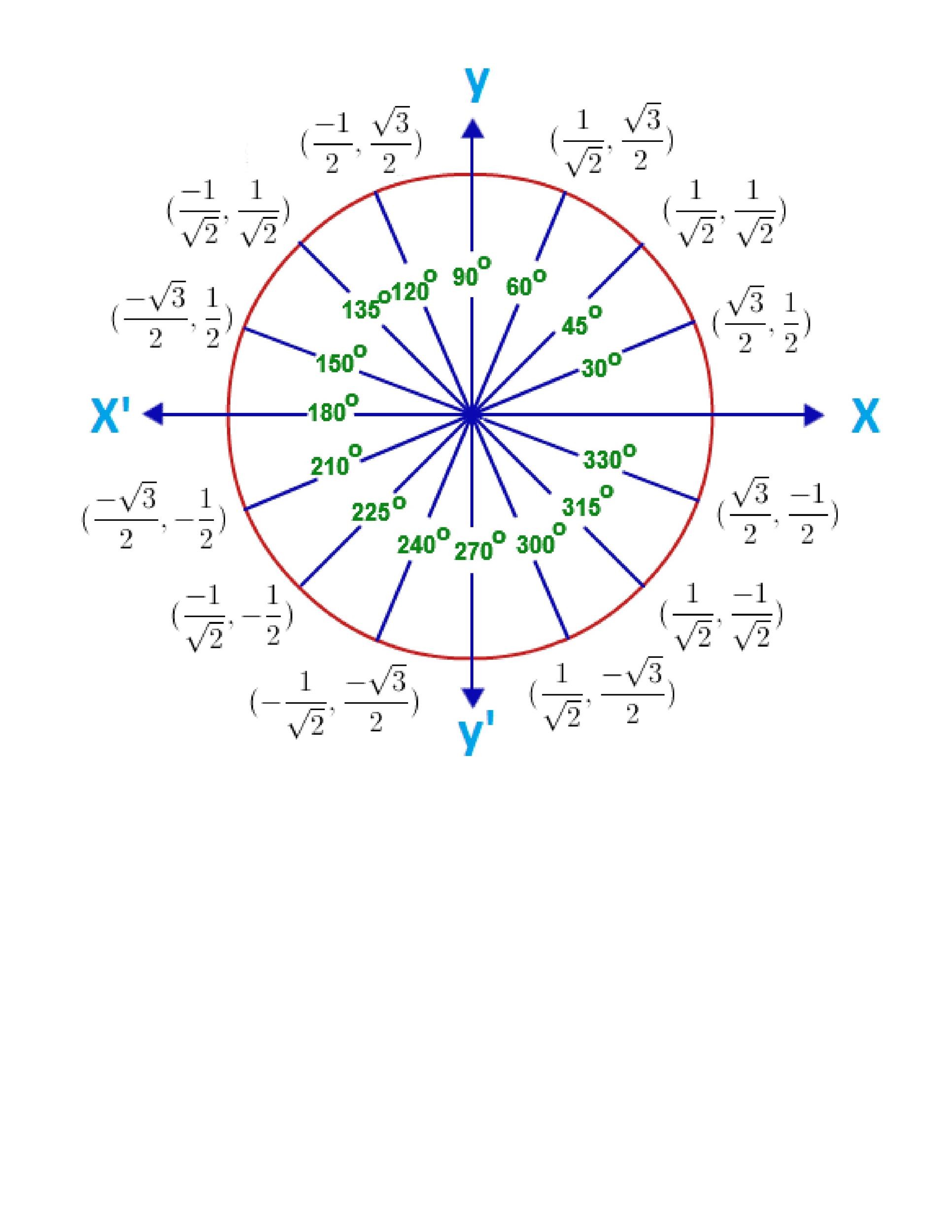
Printable Unit Circle Customize and Print
How to Use the Unit Circle in Trigonometry HowStuffWorks
Unit Circle Labeled With Special Angles And Values ClipArt ETC
Unit Circle Labeled With Quadrantal Angles And Values ClipArt ETC

Unit Circle Quick Lesson Downloadable PDF Chart · Matter of Math
Since C = 2Πr, The Circumference Of A Unit Circle Is 2Π.
The (X, Y) Coordinates Of This Point Can Be Described As Functions Of The Angle.
It Describes All The Negatives And Positive Angles In The Circle.
For A Given Angle Θ Each Ratio Stays The Same No Matter How Big Or Small The Triangle Is Trigonometry Index Unit Circle
Related Post: