What Is A Proof Drawing
What Is A Proof Drawing - From this, we see that there is an integer m (namely, 2k2) where n2 = 2m. Some proofs are impossible to solve until you add a line to the diagram. Students will make statements and reasons involving the common proof givens (midpoint, angle and segment bisector, midpoint, perpendicular lines, parallel, isosceles triangles) subjects: We want to show that n can be written as the sum of four perfect squares. Web using the new groups above method and using a proof drawing with regrouping. The figure may already be drawn for you, or you may have to draw it yourself. By drawing a rectangle of side length a and b, we can see that the area a b is the same as the area ba. Web the following proof introduces you to a new idea: Opposite angles of a parallelogram. This is a proof without words. This is a great way to introduce proofs. You must have a reason for every statement. Web a proof is a rigorous argument that shows a mathematical claim to be true. A proof drawingencer is used for verifying or proving the existence of an object or concept. This states the theorem to be proved. Web writing a proof consists of a few different steps. Since n is even, there is some integer k such that n = 2k. Stands for “ épreuve d’artiste ,” meaning artist’s proof in french. Web the proof we just saw of pythagoras’ theorem is an example of a direct proof. This states the theorem to be proved. In this section we are going to look at a different type of proof, called a proof by contradiction. What formula does figure (3) prove? Stands for hors commerce, or “not to sell.” similar to an artist’s proof, this proof was set aside from the editioned prints. Proof:let n be an even integer. A proof drawingencer is created by using. Draw the figure that illustrates what is to be proved. Such lines are called auxiliary lines. Students will make statements and reasons involving the common proof givens (midpoint, angle and segment bisector, midpoint, perpendicular lines, parallel, isosceles triangles) subjects: You must have a reason for every statement. Auxiliary lines often create congruent triangles, or they intersect existing lines at right. The kids ungroup rather than borrow. Web using the new groups above method and using a proof drawing with regrouping. List the given statements, and then list the conclusion to be proved. Direct proofs and indirect proofs. Web a proof is a rigorous argument that shows a mathematical claim to be true. Web a proof is a rigorous argument that shows a mathematical claim to be true. Rhombus diagonals are perpendicular bisectors. You must have a reason for every statement. There are two major types of proofs: Direct proofs and indirect proofs. The order of the statements in the proof is not always fixed, but make sure the order makes logical sense. Proof:let n be an even integer. A small square is drawn at the right margin at the end of the proof to signify that the proof is complete. This is a great way to introduce proofs. See the other videos. Auxiliary lines often create congruent triangles, or they intersect existing lines at right angles. Web what is an artists proof? Ea (épreuve d’artiste) means “artist proof” in french Since n is even, there is some integer k such that n = 2k. This is a proof without words. Sometimes you have to translate the statement of the theorem into the specifics of your drawing. If n is an even integer, then n2 is even. Reasons will be definitions, postulates, properties and previously proven theorems. Web the following proof introduces you to a new idea: Web what is the purpose of a proof drawing. Stands for hors commerce, or “not to sell.” similar to an artist’s proof, this proof was set aside from the editioned prints. This states the theorem to be proved. This symbol means “end of proof” this. Web the proof definition in geometry is a chain of deductions through which the truth of given statements is verified. Web a proof is. Web what is a design proof? In this section we are going to look at a different type of proof, called a proof by contradiction. This states the theorem to be proved. Proof:let n be an even integer. ( the actual logic of the proof goes here ) thus n is the sum of four perfect squares, as required. A small square is drawn at the right margin at the end of the proof to signify that the proof is complete. It is most commonly used for drawings of fictional objects, such as guns or clubs. The kids ungroup rather than borrow. Web writing a proof consists of a few different steps. Web the proof definition in geometry is a chain of deductions through which the truth of given statements is verified. From this, we see that there is an integer m (namely, 2k2) where n2 = 2m. Opposite angles of a parallelogram. The order of the statements in the proof is not always fixed, but make sure the order makes logical sense. This video shows how we use proof drawings for subtraction. Now you have a beginning and an end to the proof. Web what is the purpose of a proof drawing.
How to make a proof drawing math strategy YouTube

What Is A Proof Drawing Math 2nd Grade Homey Gears
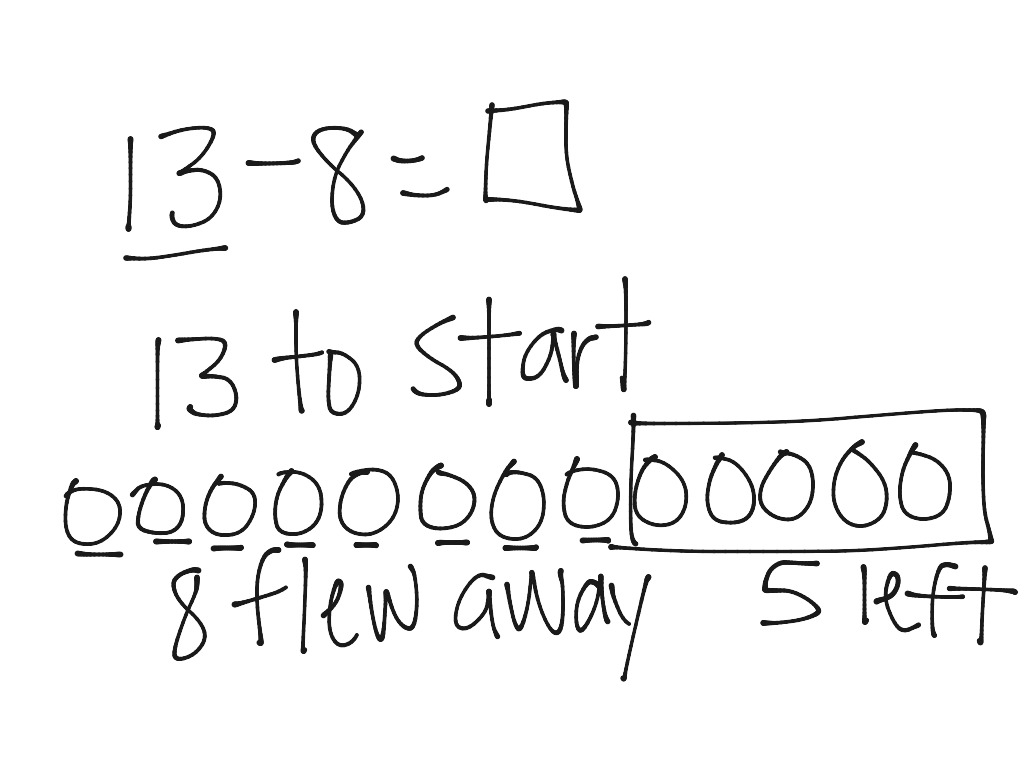
Proof Drawing Math, Elementary Math, 2nd Grade Math ShowMe
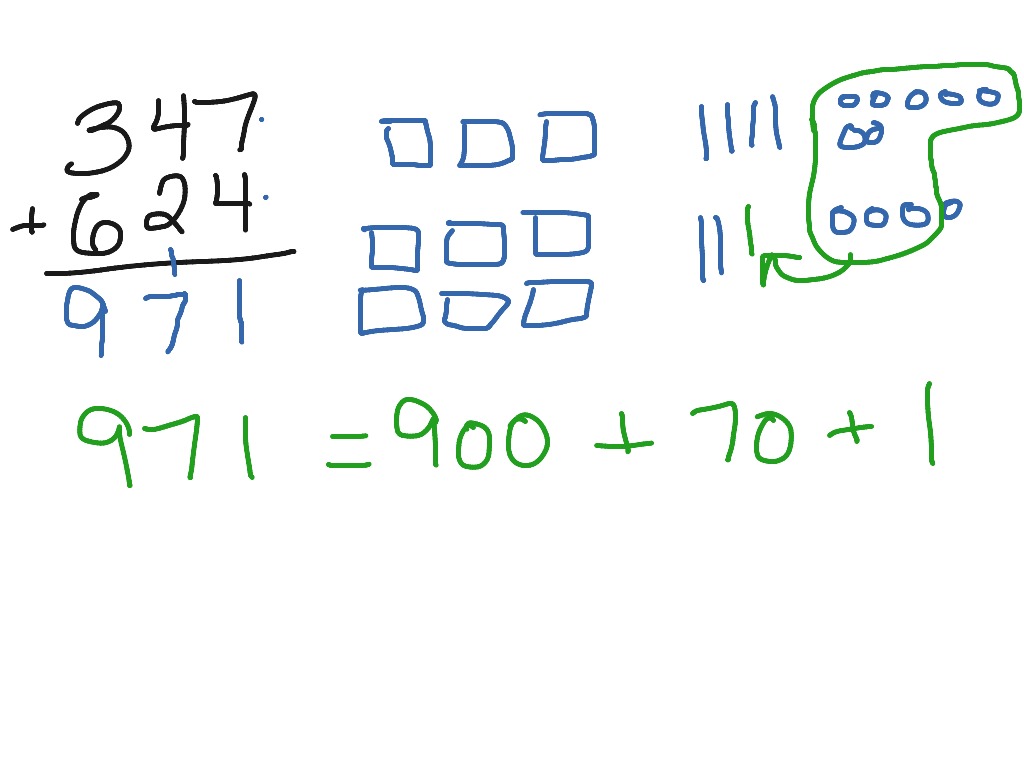
Third gradeunit 4 adding with proof drawings Math, Elementary Math

Addition Proof Drawing for Word Problems YouTube

How To Do A Proof Drawing Warehouse of Ideas
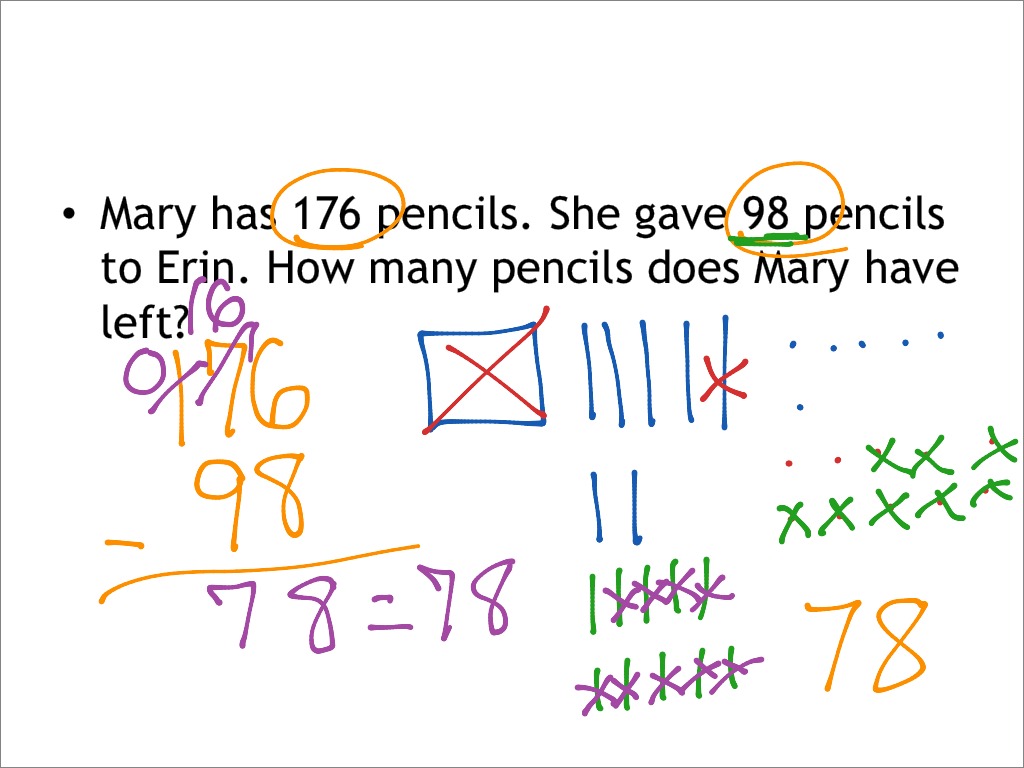
Proof drawing Math, Elementary Math, 3rd grade, subtraction ShowMe

proof drawing 2nd grade math howtotieashirtknotmaternity

Math Subtraction Proof Drawing YouTube

Proof Drawings Ungrouping to Subtract Subtraction, 2nd grade math, Math
Web Using The New Groups Above Method And Using A Proof Drawing With Regrouping.
The Diagonals Of A Kite Are Perpendicular.
By Drawing A Rectangle Of Side Length A And B, We Can See That The Area A B Is The Same As The Area Ba.
Here, We Use Learned Concepts, Facts, And Methods To Prove The Statement Given.
Related Post: