What Is The Lateral Area Of The Drawing
What Is The Lateral Area Of The Drawing - Web a_l = π x r x √ (r² + h²) or, in terms of the cone's slant: As you can see the shape has all four lateral faces of the same rectangular form with the same sides lengths, therefore, answer: Web civil engineering civil engineering questions and answers what's the lateral area of the drawing? Length = 7 m width = 7 m height = 6.1 m plugging in the values: Total surface area lateral area area of bases=+2 11( )( ) ( )( ) =+ +72 34 34 22 7266=++ 84= cm2 there is a bit of a shortcut for finding the lateral area of a prism. The lateral area is also referred to as the lateral surface area (lsa) and is always measured in square units. It is also called lateral surface area (lsa) or curved surface area (csa) of a cone. Europeans' desire for less control from a central government and greater local political autonomy is an example of a. Etymologically, lateral refers to side, which, in geometry,. What's the lateral area of the drawing? Web what is the lateral area of the drawing? Since we have given 4 trapeziums with parallel sides : Web a_l = π x r x √ (r² + h²) or, in terms of the cone's slant: What's the lateral area of the drawing? Where π = 22/7 or 3.14, r = radius of a cylinder, and h is the. This problem has been solved! You'll get a detailed solution from a subject matter expert that helps you learn core concepts. What's the lateral area of the drawing? Each of the 6 faces is a square 7 m on the edge. Web learn practice download lateral area of a cone the lateral area of a cone is defined as the. Europeans' desire for less control from a central government and greater local political autonomy is an example of a. Lateral area = 2 * (length * width) + 2 * (length * height) + 2 * (width * height) given the dimensions of the object: What is the difference between lateral area and surface area? Since we have given 4. (7 m)² = 49 m². What's the lateral area of the drawing? What's the lateral area of the drawing? And we have 4 lateral sides. Each side is an isosceles trapezoid, so ed=2 since you would need to add 2 to each end of the bottom line to get the top line. Web the lateral area can be calculated as: This problem has been solved! The area of the lateral face that is rectangle with sides 5 mi and 2 mi is. Since we have given 4 trapeziums with parallel sides : 6 × 49 m² = 294 m². The lateral area of the prism is 294 m². Web the lateral area formula is used to find the lateral area of any solid object. The lateral area of the drawing is 40 mi2. Web a_l = π x r x √ (r² + h²) or, in terms of the cone's slant: Web the lateral surface area of an object. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. What's the lateral area of the drawing? This is the height of each trapezoid. 6 × 49 m² = 294 m². In the lateral area formula, the base area of the object as well as that of the face parallel to the base are. The greater wings of sphenoid bone are lateral projections of the sphenoid bone. The lateral area of the prism is 294 m². This answer has been confirmed as correct and helpful. Web the lateral area of the drawing refers to the side view or the external surface of the object being depicted. You'll get a detailed solution from a subject. A_l = π x r x l where: Web answer answered what is the lateral area of the drawing? What's the lateral area of the drawing? For example, a cylinder of height h and radius r has a ′ = π r 2 {\displaystyle a'=\pi r^{2}} when viewed along its central axis, and a ′ = 2 r h {\displaystyle. Now use pythagorean theorem to get ed^2+ad^2=ae^2. It is also called lateral surface area (lsa) or curved surface area (csa) of a cone. Web we know that the area of a rectangle is the product of its sides, then, in this case, each of the lateral rectangles has an area of 5mi*2mi = 10mi^2. This is the height of each. The lateral area is the sum of the areas of the 6 square faces. Web a_l = π x r x √ (r² + h²) or, in terms of the cone's slant: Web the lateral area of the drawing refers to the side view or the external surface of the object being depicted. Web we know that the area of a rectangle is the product of its sides, then, in this case, each of the lateral rectangles has an area of 5mi*2mi = 10mi^2. Plug in your numbers to solve for ae. A_l = π x r x l where: Web civil engineering civil engineering questions and answers what's the lateral area of the drawing? This answer has been confirmed as correct and helpful. Lateral area = 2 * (7 m * 7 m) + 2 * (7 m * 6.1 m) + 2 * (7 m * 6.1 m) = 2 * 49 m² + 2 * 42.7 m² + 2 * 42.7 m² = 98 m². In this case, based on the provided information, the drawing is of the greater wings of sphenoid bone. What's the lateral area of the drawing? (image will be uploaded soon) lateral surface area of. Then the area of the lateral sides is 4*10mi^2 = 40mi^2 then the correct answer is c. Web learn practice download lateral area of a cone the lateral area of a cone is defined as the area covered by the curved surface of the cone. Web lateral area refers to the surface area of a 3d object such as prism, cylinder, cone etc., lateral surface area is the sum of all sides of a 3d object except its top and bottom bases. The area of the lateral face that is rectangle with sides 5 mi and 2 mi is.
PPT Lateral Area, Surface Area, and Volume Notes PowerPoint

what is the lateral area of the drawing
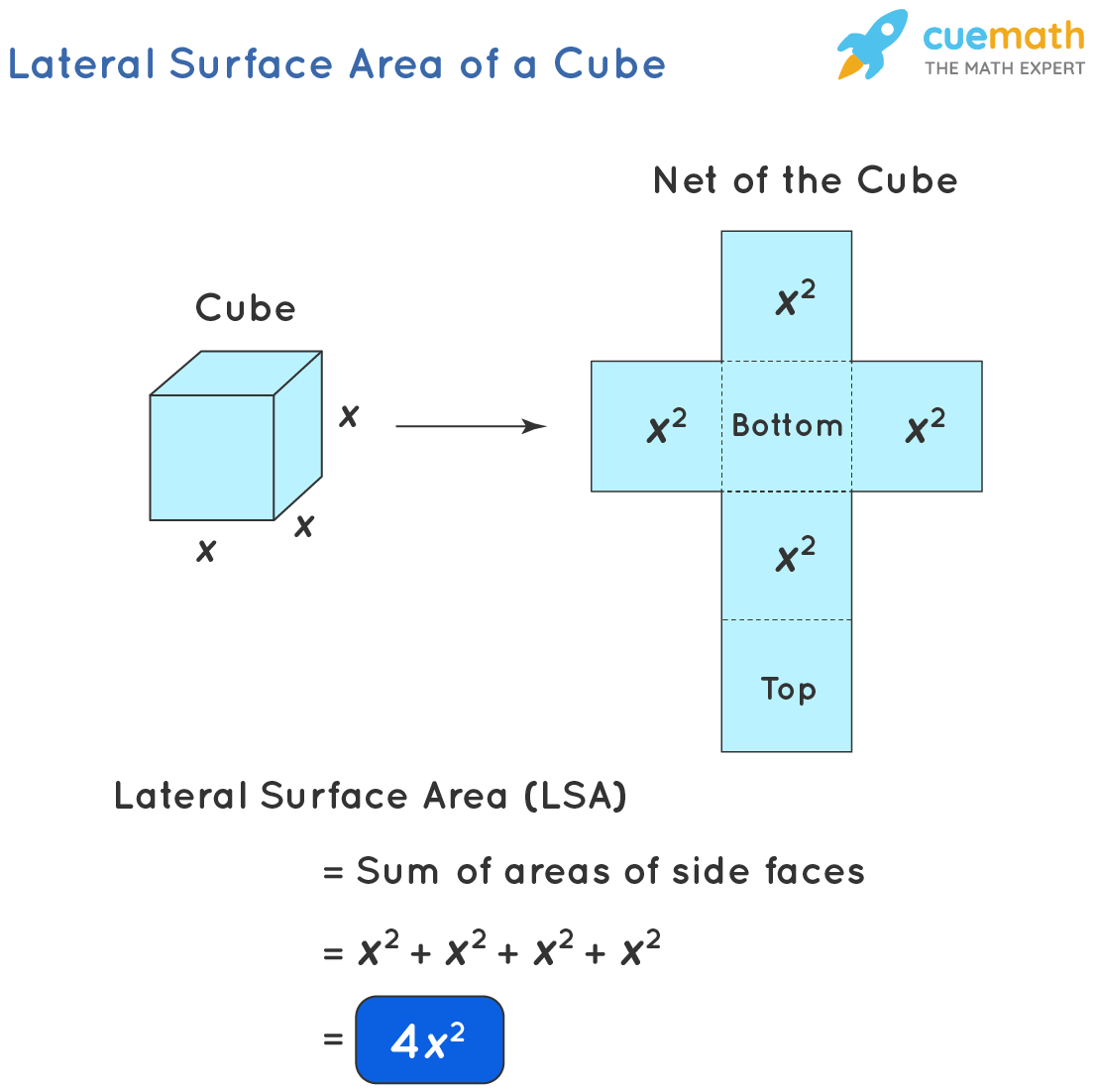
Lateral Surface Area of a Cube Formula, Examples, Definition
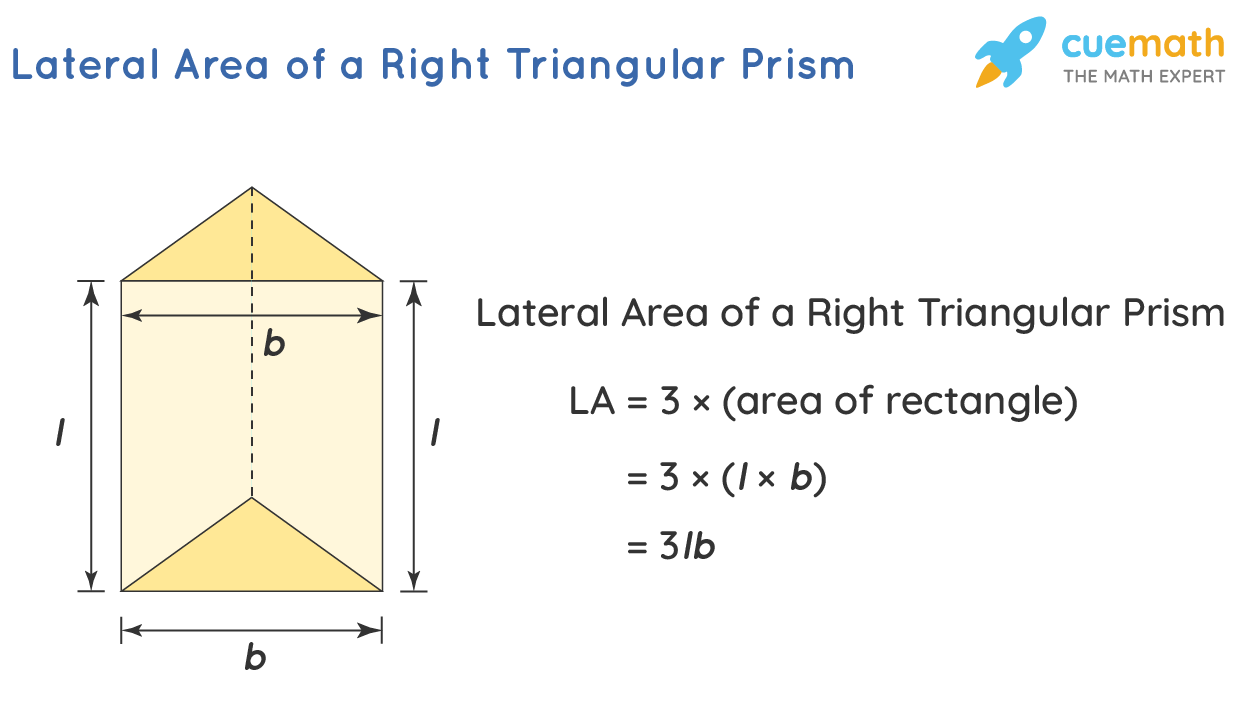
Lateral Area of a Right Triangular Prism Formula, Examples
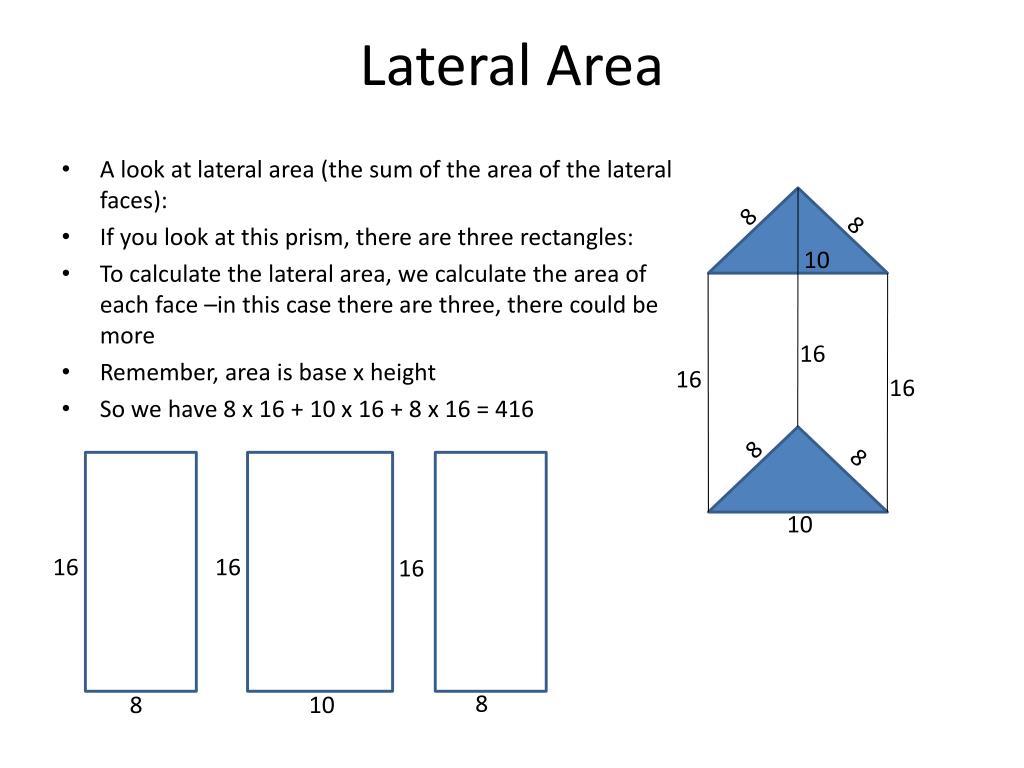
How To Find Lateral Area Of Triangular Prism Haiper

what is the lateral area of the drawing
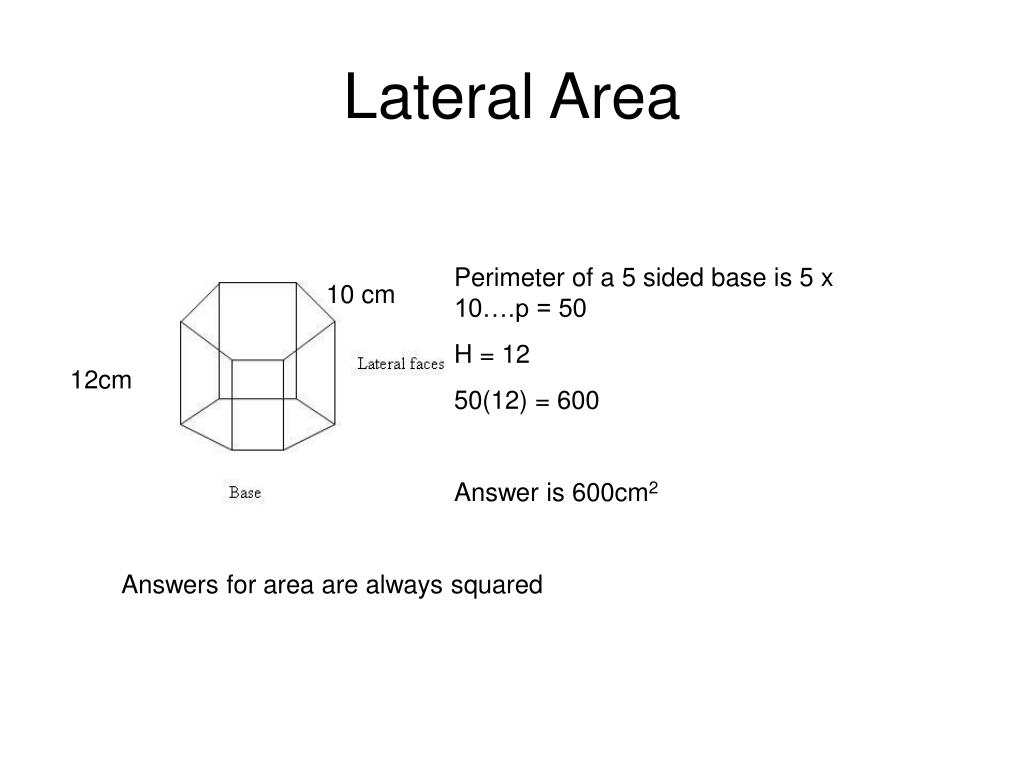
PPT Lateral Area, Surface Area, and Volume Notes PowerPoint

what is the lateral area of the drawing

Lateral Area Definition, Formula & Examples Video & Lesson
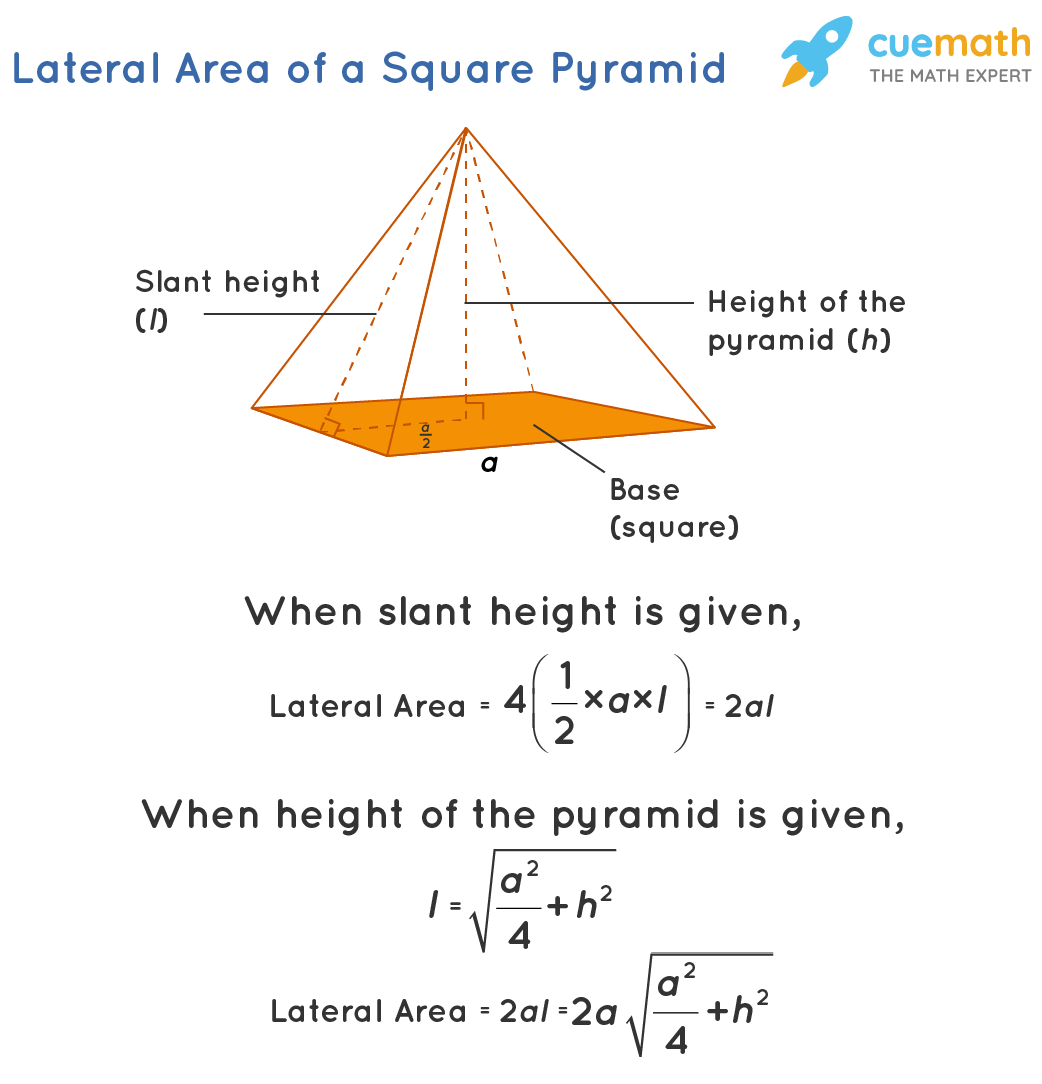
Lateral Area of a Square Pyramid Formula, Examples, Definition
6 × 49 M² = 294 M².
Total Surface Area Lateral Area Area Of Bases=+2 11( )( ) ( )( ) =+ +72 34 34 22 7266=++ 84= Cm2 There Is A Bit Of A Shortcut For Finding The Lateral Area Of A Prism.
Lateral Area = 2 * (Length * Width) + 2 * (Length * Height) + 2 * (Width * Height) Given The Dimensions Of The Object:
For Example, A Cylinder Of Height H And Radius R Has A ′ = Π R 2 {\Displaystyle A'=\Pi R^{2}} When Viewed Along Its Central Axis, And A ′ = 2 R H {\Displaystyle A'=2Rh} When Viewed.
Related Post: